ピタゴラスの定理

直角三角形において、斜辺の長さを \( c \)、他の2辺の長さを \( a, b \) とすると、次の式が成り立つ：\[ a^2 + b^2 = c^2 \]

直角三角形 \(ABC\) を考え、直角を \(B\) に取る。各辺の長さを \( AB = a, BC = b, AC = c \) とする。

この三角形を\(4\)つ用意し、これらを大きな正方形の内部に組み合わせて配置する。

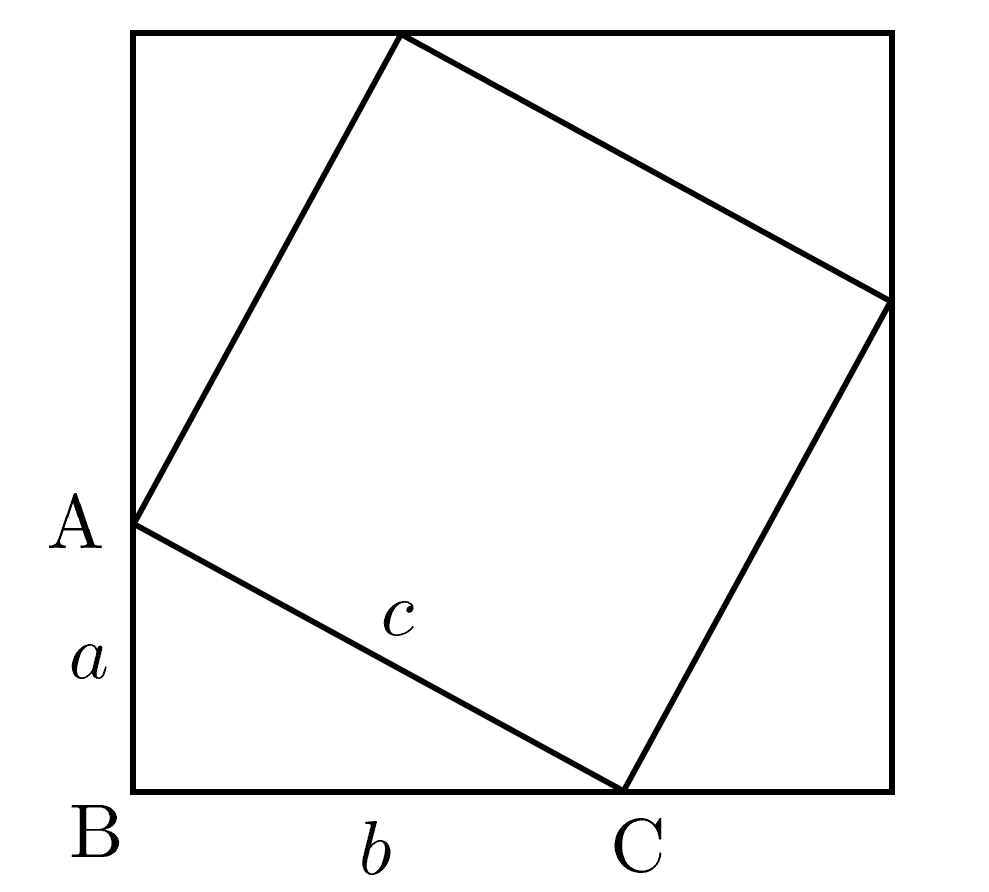
大きな正方形の一辺の長さは \( a + b \) であり、その面積は\( (a+b)^2 \)である。

この正方形の内部には、\(4\)つの直角三角形と、中央にできる小さな正方形が含まれる。小さな正方形の一辺の長さは \( c \) である。

各直角三角形の面積は \( \frac{1}{2} ab \) であり、\(4\)つあるので合計の面積は、

\[ 4 \times \frac{1}{2} ab = 2ab \]

また、中央の小さな正方形の面積は、\( c^2 \)である。

よって、大きな正方形の面積は、4つの三角形の面積と中央の正方形の面積の和に等しいことより、

\[ (a+b)^2 = 2ab + c^2 \]

左辺を展開して、

\[ a^2 + 2ab + b^2 = 2ab + c^2 \]

両辺から \( 2ab \) を引くと、

\[ a^2 + b^2 = c^2 \]

したがって、ピタゴラスの定理が証明された。(証明終)

応用問題

直角三角形の一辺の長さが3cm、もう一辺の長さが4cmのとき、斜辺の長さを求めよ。

解答

ピタゴラスの定理より、斜辺の長さ \( c \) は次のように求められる：

\( c^2 = 3^2 + 4^2 = 9 + 16 = 25 \)

したがって、\( c = \sqrt{25} = 5 \) cm

直角三角形の斜辺の長さが13cm、一辺の長さが5cmのとき、残りの一辺の長さを求めよ。

解答

ピタゴラスの定理より、残りの一辺の長さ \( b \) は次のように求められる：

\( 13^2 = 5^2 + b^2 \)

\( 169 = 25 + b^2 \)

\( b^2 = 144 \)

したがって、\( b = \sqrt{144} = 12 \) cm

長さが10cmのはしごを、床と壁に立てかけたところ、はしごの上端が壁から高さ8cmの位置にあった。このとき、はしごの下端が壁からどれだけ離れているか求めよ。

解答

壁からの距離を \( x \) cm とすると、直角三角形ができる。

ピタゴラスの定理より：

\( 10^2 = 8^2 + x^2 \)

\( 100 = 64 + x^2 \)

\( x^2 = 36 \)

したがって、\( x = \sqrt{36} = 6 \) cm